
Understanding the Structural Design of Beams
In civil and structural engineering, beams play a crucial role in supporting loads and maintaining the integrity of various structures. The design and dimensions of a beam, particularly its depth and breadth, are essential factors that directly impact its performance. A common observation in beam design is that the depth of a beam is significantly greater than its breadth. This article delves into the reasons behind this design choice and explains why the breadth of a beam is typically shorter than its depth.
Table of Contents
The Basic Concept: Resistance to Bending
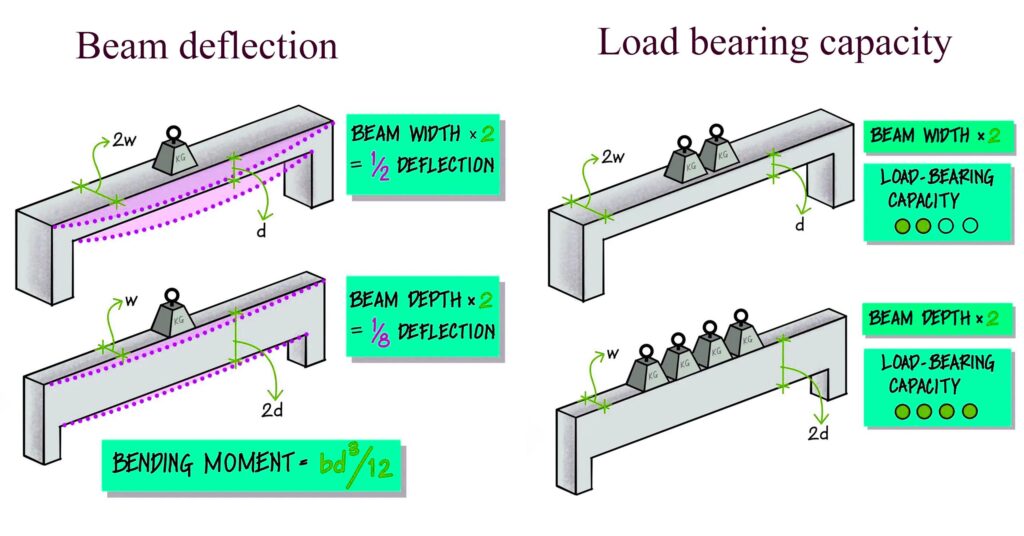
When a beam is subjected to loads, it experiences bending. The resistance of a beam to bending is a key factor in determining its ability to support the applied loads without undergoing excessive deflection. The efficiency of a beam in resisting bending depends on how its material is distributed relative to the bending axis, which is quantified by the area moment of inertia (also known as the second moment of area).
Area Moment of Inertia and Its Importance
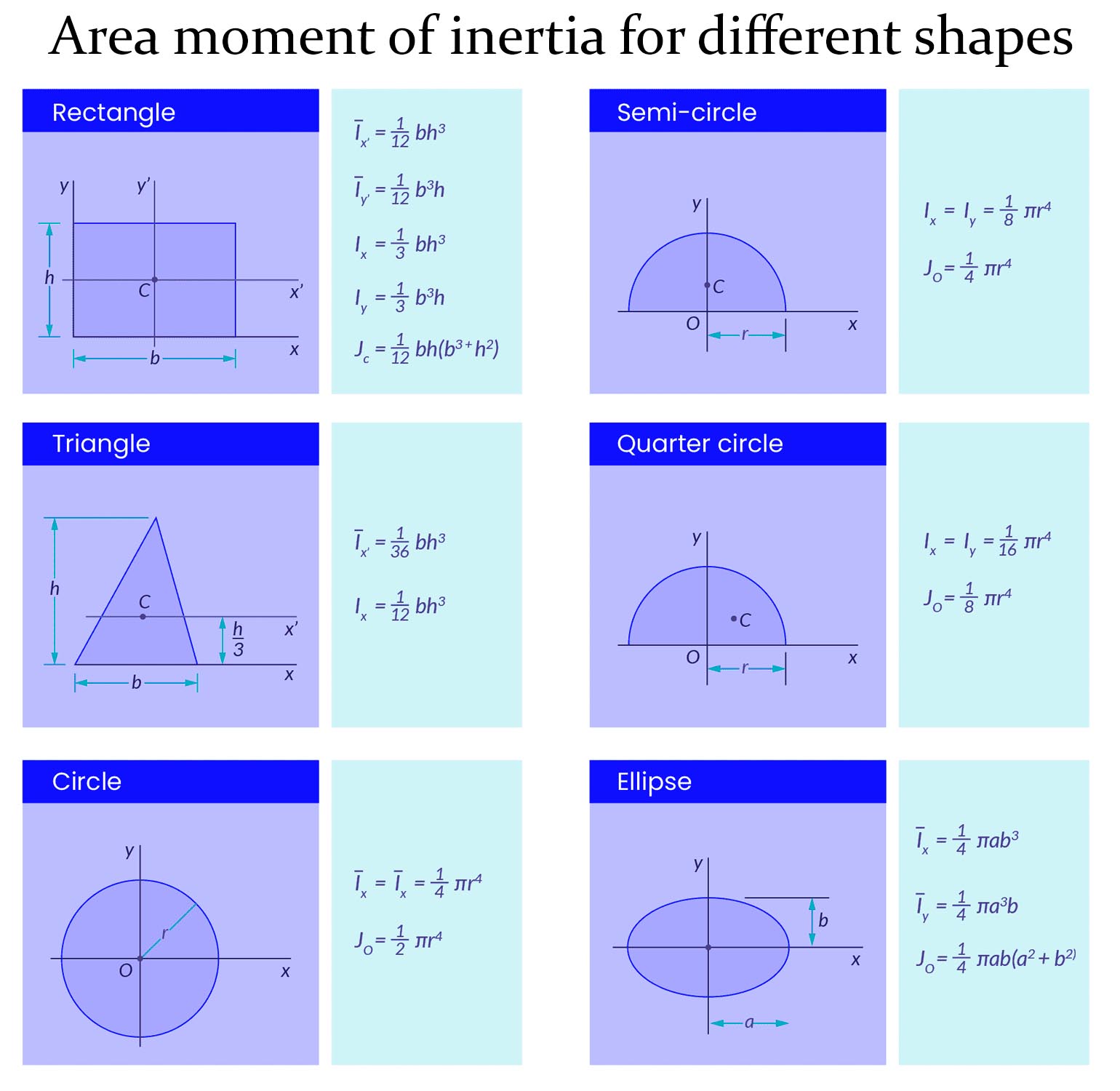
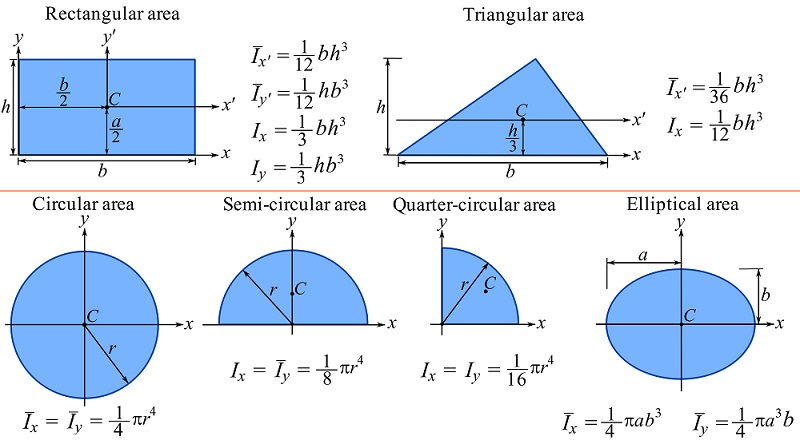
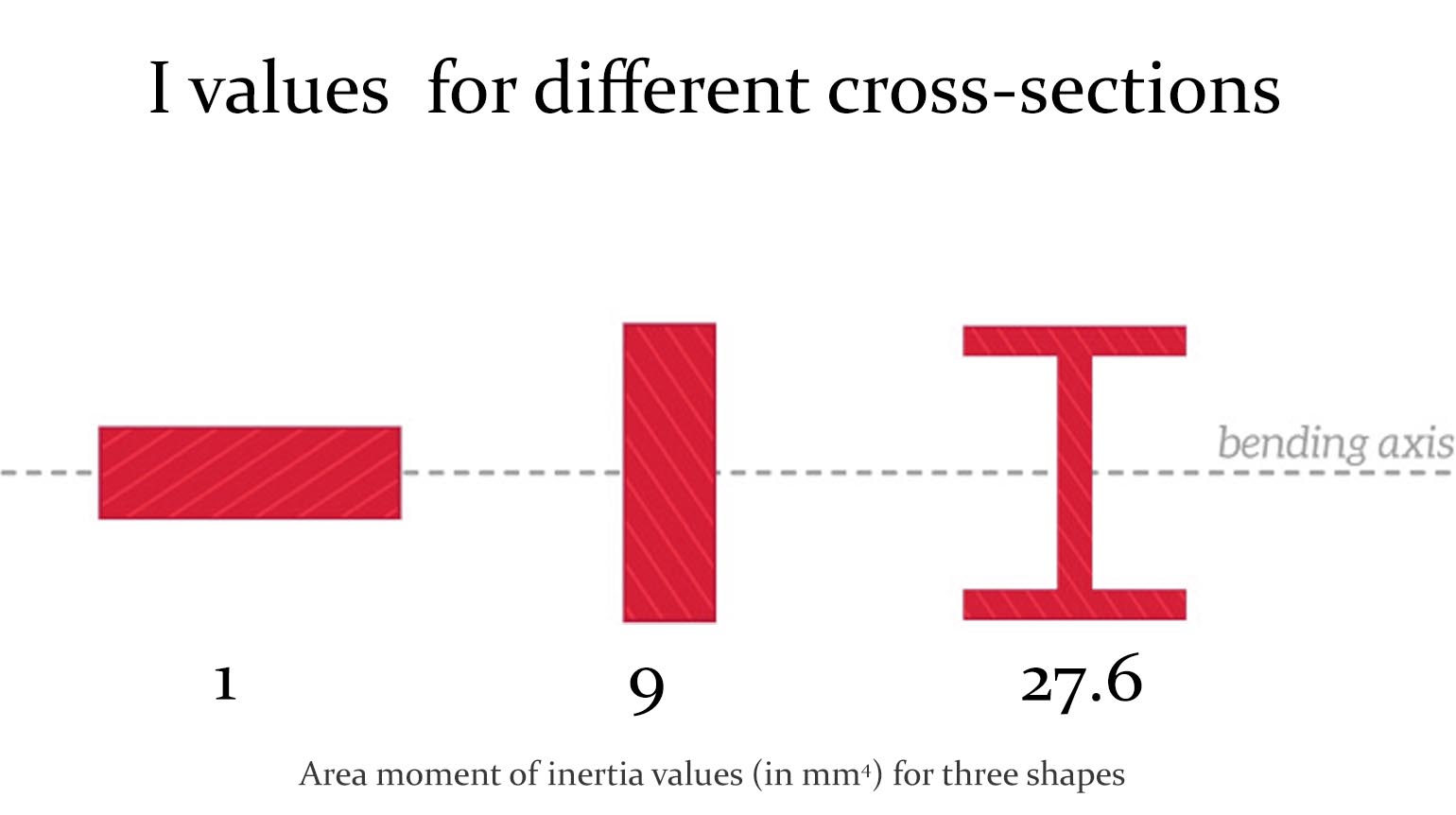
The area moment of inertia (I) (mm4 or in4) is a geometric property that reflects the distribution of a cross-sectional area relative to a specific axis. It plays a pivotal role in determining the stiffness of a beam and its ability to resist bending. The higher the area moment of inertia, the more resistant the beam is to bending.
For a rectangular cross-section, the formula for the moment of inertia is given by:
I = bd³/12
Where:
- b = breadth of the beam
- d = depth of the beam
From this formula, it is evident that the moment of inertia increases linearly with the breadth (b) but increases by the cube of the depth (d). This means that even a small increase in the depth of the beam significantly enhances its resistance to bending.
Why Is Depth More Important Than Breadth?
Given the formula for the moment of inertia, we can see that increasing the depth of the beam has a more pronounced effect on its ability to resist bending than increasing its breadth. This is because the depth is raised to the third power (cubed) in the formula, whereas the breadth is only multiplied linearly. As a result, a deeper beam can support greater loads and experience less deflection than a beam with a wider but shallower cross-section.
Flexural Stress and Its Implications
The performance of a beam under load is also governed by the concept of flexural stress. The flexural stress (σ) in a beam is given by the formula:
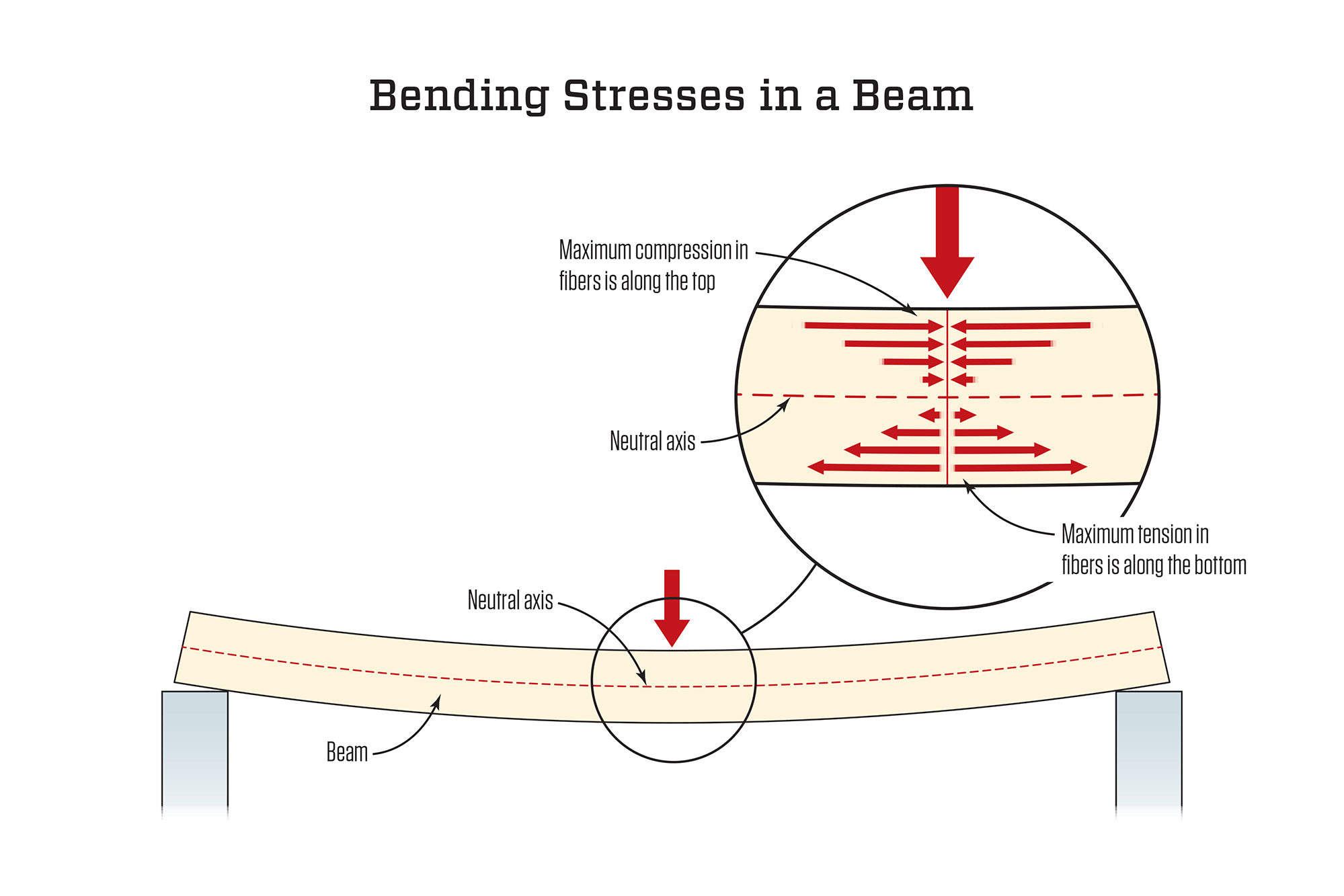
σ = My/I
Where:
- M = bending moment
- y = distance from the neutral axis to the outermost fiber
- I = moment of inertia
- σ = Bending stress (flexural stress)
Flexural stress increases as the bending moment (M) and the distance from the neutral axis (y) increase. However, it decreases as the moment of inertia (I) increases. This relationship highlights the importance of maximizing the moment of inertia (I) to minimize flexural stress, which can be effectively achieved by increasing the depth of the beam.
Practical Application: Why Beams Are Designed With Greater Depth
Load-Bearing Capacity and Deflection Control
In real-world applications, beams are designed to carry loads while minimizing deflection. The deflection of a beam under load can lead to structural issues, including cracking, excessive sagging, and even failure. By increasing the depth of the beam, engineers can enhance its load-bearing capacity and reduce deflection. This is why beams used in construction, such as I-beams and T-beams, are designed with greater depth relative to their breadth.
Material Efficiency and Cost-Effectiveness
Another reason for prioritizing depth over breadth in beam design is material efficiency. By increasing the depth, the beam can achieve the required strength and stiffness with less material, making the design more cost-effective. This is particularly important in large-scale construction projects where material costs are a significant consideration.
Example: Comparing Beams with Different Depths and Breadths
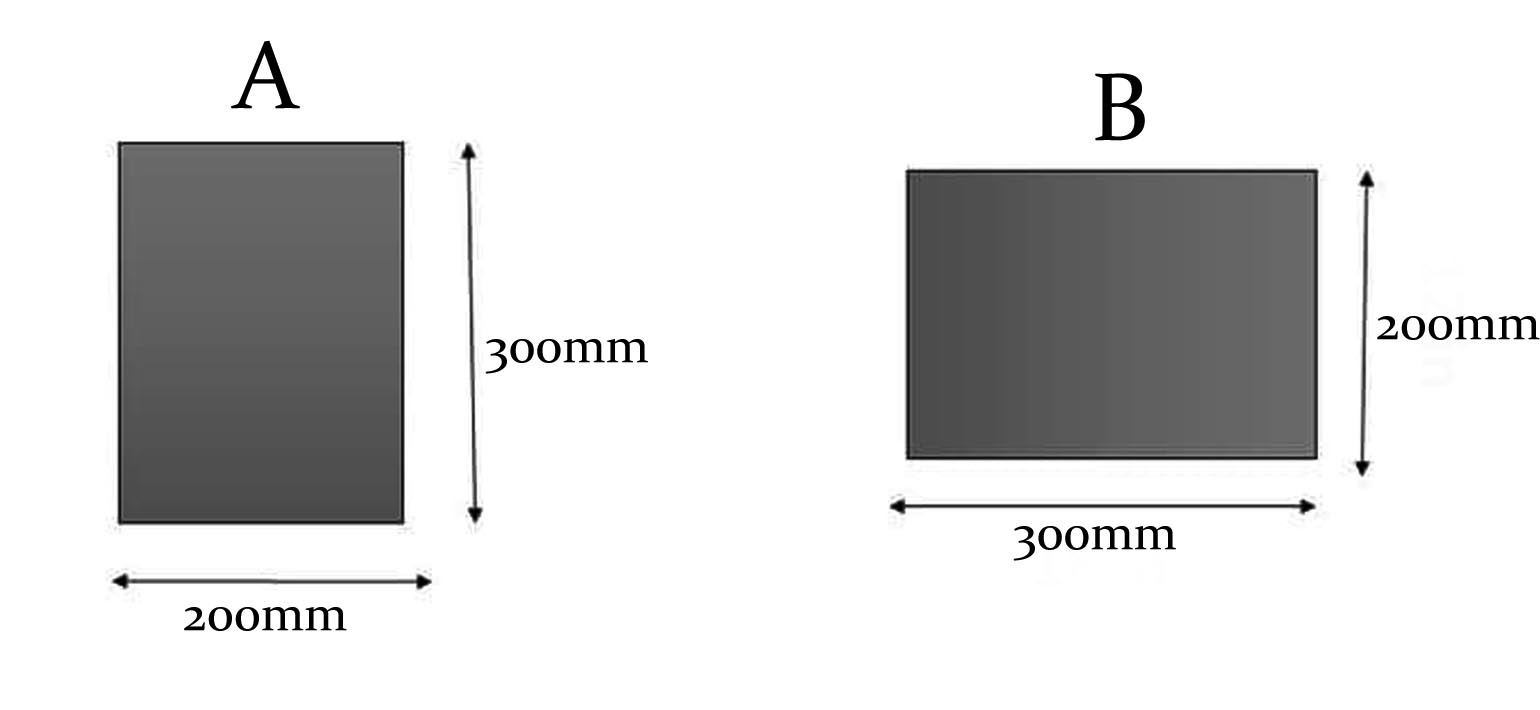
To illustrate the impact of depth on the performance of a beam, consider two beams with the same cross-sectional area but different dimensions. Beam A has a breadth of 200 mm and a depth of 300 mm, while Beam B has a breadth of 300 mm and a depth of 200 mm.
I = bd³/12
For Beam A:
- I = (200 * 300³)/12 = 450,000,000 mm⁴
For Beam B:
- I = (300 * 200³)/12 = 200,000,000 mm⁴
Despite having the same cross-sectional area, Beam A has a much higher moment of inertia (450,000,000 mm⁴) compared to Beam B (200,000,000 mm⁴). This means Beam A is more resistant to bending and will exhibit less deflection under the same load, demonstrating the advantage of having greater depth.
