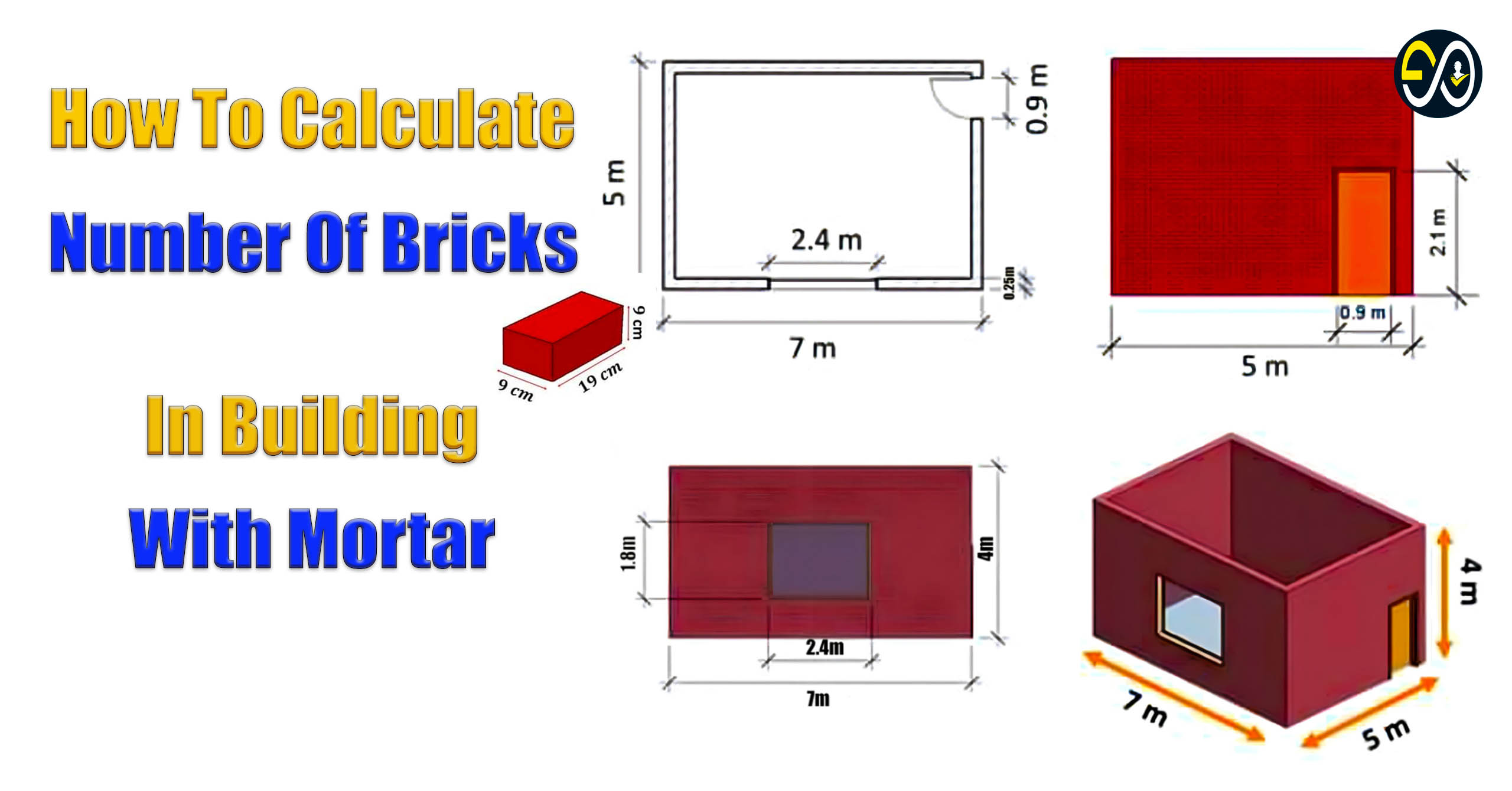
When we are tasked with any construction project, calculating the volume of concrete is a crucial aspect of planning. The concrete mix we are considering today is the M20 grade concrete, which is commonly used in residential and small commercial buildings. This type of concrete consists of a mix ratio of 1:1.5:3. Let’s break down the process step by step to make accurate calculations, ensuring that we have the correct amount of materials for our concrete mix.
Understanding M20 Grade Concrete
Before we dive into the calculations, let’s clarify what M20 concrete represents. According to the IS456:2000 standard, M20 concrete refers to a mixture of cement, sand (fine aggregates), and coarse aggregates in the ratio of 1:1.5:3. This means:
- 1 part cement
- 1.5 parts sand
- 3 parts aggregates

This grade of concrete has a compressive strength of 20 N/mm2 (20 MPa) after 28 days of curing, which is suitable for moderate structural applications.
Step 1: Calculating the Dry Volume of Concrete
One of the essential first steps in determining how much material you need is calculating the dry volume of the concrete. This is because the actual volume of required dry material is always higher than the wet volume due to the air gaps between the particles of cement, sand, and aggregates.
To adjust for this, we multiply the wet volume by a factor of 1.54 to account for the bulking of sand and wastage:
Dry Volume = Wet Volume x 1.54
For 1 m3 of concrete, the dry volume is calculated as:
Dry Volume = 1 x 1.54 = 1.54 m3
Step 2: Estimating the Quantity of Cement, Sand, and Aggregate
Now that we know the dry volume, we need to calculate the quantity of cement, sand, and aggregate required based on the 1:1.5:3 ratio.
Cement Calculation:
The cement part in the ratio is 1. Therefore, the volume of cement needed is:
Cement Volume = (1/1 + 1.5 + 31) x1.54
Cement Volume = (1/5.5) x 1.54 = 0.28m3
To convert cubic meters to bags of cement, use the conversion factor: 1 m3 = 1440 kg of cement. One bag of cement weighs 50 kg, so:
Cement in Bags = (0.28 x 1440)/50 = 8 Bags (approximately)
Sand (Fine Aggregate) Calculation:
The sand part in the ratio is 1.5. Therefore, the volume of sand needed is:
Sand Volume = (1.5/5.5) x 1.54
Sand Volume = 0.42m3
1m3 = 1600 kg of sand
0.42 x 1600 = 672 kg
Weight of 1 CFT Sand = 43.30 kg
672/43.30 ≈ 16 ft3
Aggregate (Coarse Aggregate) Calculation:
The aggregate part in the ratio is 3. Therefore, the volume of coarse aggregate needed is:
Aggregate Volume = (3/5.5) x 1.54
Aggregate Volume = 0.84m3
1m3 = 1800 kg of aggregate
0.84 x 1800 = 1512 kg
Weight of 1 CFT Aggregate = 68.15 kg
1512/68.15 ≈ 22 ft3
Step 3: Calculating the Amount of Water
The water-cement ratio is a crucial factor affecting the concrete’s strength and workability. For M20-grade concrete, a typical water-cement ratio is around 0.5.
Using this ratio, we calculate the amount of water needed for the mix:
Water Volume = Cement Volume x Water-Cement Ratio
Water Volume = 0.28m3 x 0.5 = 0.14m3
To convert this to liters (since 1m3 = 1000 liters), we get:
Water Volume = 0.14 x 1000 = 140 liters
Step 4: Summary of Material Requirements
For 1 m³ of M20-grade concrete, the material quantities required are:
- Cement: 8 bags (approximately)
- Sand: 0.42 m3
- Coarse Aggregates: 0.84 m3
- Water: 140 liters
These quantities ensure a proper mix ratio of 1:1.5:3, suitable for M20-grade concrete, and provide adequate strength for moderate structural applications.
Additional Considerations for Concrete Mix Calculations
- Wastage: It’s advisable to account for a small percentage of wastage, typically around 2% to 5%, depending on the project and site conditions.
- Transportation and Workability: While calculating, ensure that the concrete is mixed efficiently, whether on-site or in a batching plant, to maintain workability without compromising strength.
- Testing: After mixing the concrete, always test its slump and strength to verify that it meets the design requirements.
- Curing: After pouring, ensure that the concrete is properly cured for at least 28 days to achieve the desired strength.