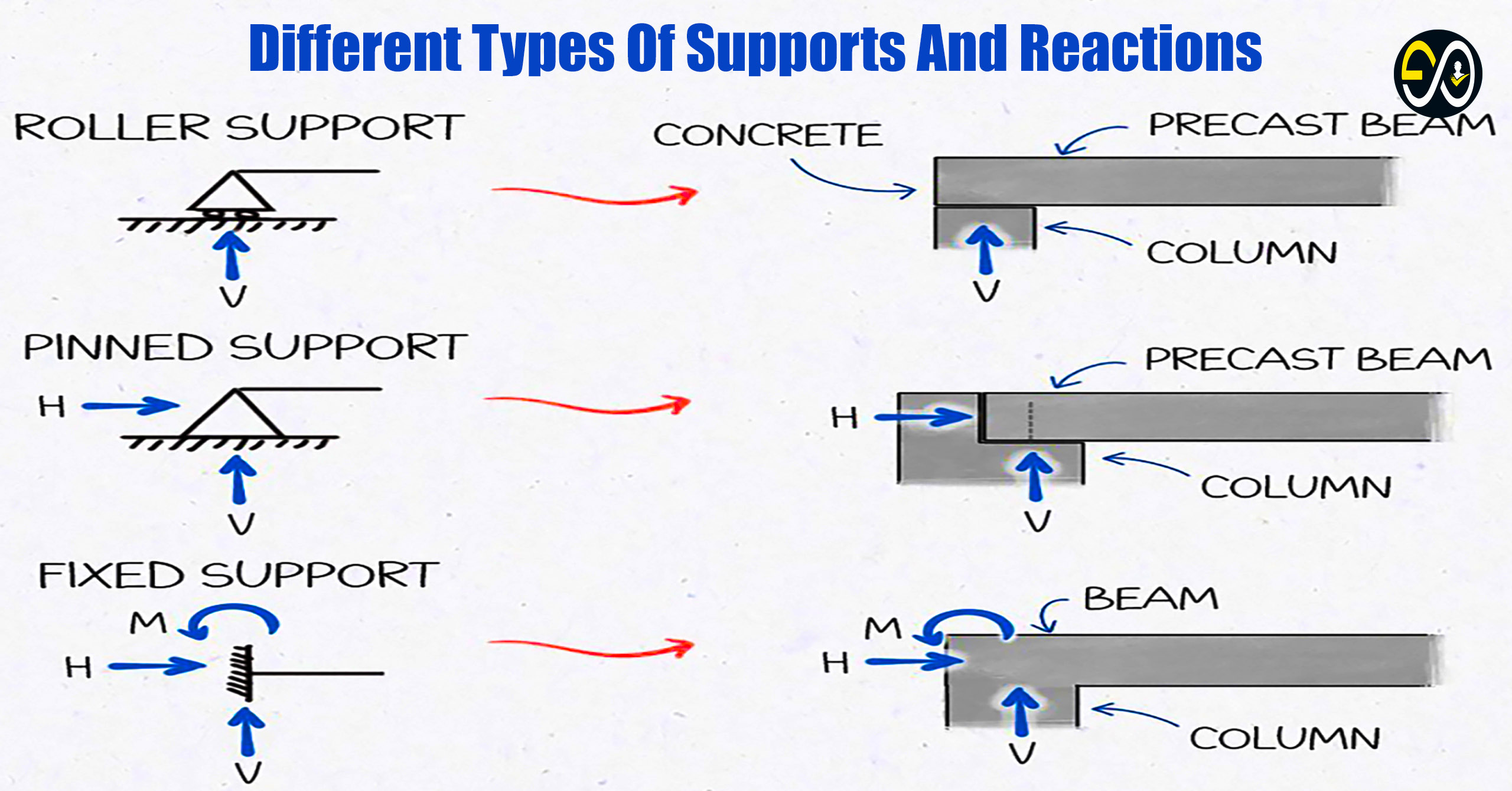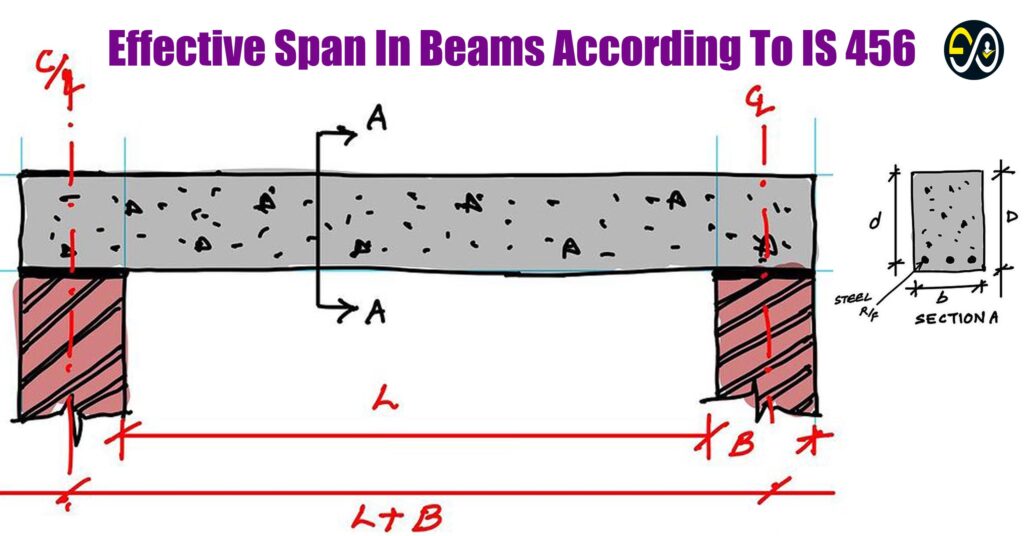
In structural engineering, the concept of the effective span of a beam is crucial for ensuring the structural integrity and safety of buildings. Clause 22.2 in IS 456 outlines the calculation methods for effective spans, particularly in supported beams and slabs. This standard provides essential guidance for structural engineers, architects, and builders, ensuring that constructions are safe and efficient in material use. This article dives into Clause 22.2, explaining the effective span concept, calculation methods, and practical applications.
What is the Effective Span of a Beam?
The effective span of a beam or slab is the distance that governs the bending moments and shear forces in structural analysis. It determines the length of the member that actively contributes to supporting loads. Accurate calculation of effective spans is essential because it directly influences the structure’s strength, stiffness, and material economy. The effective span is often slightly longer than the clear span (the unobstructed distance between supports) due to the allowance for partial embedment at the supports.
Clause 22.2 of IS 456: Calculating Effective Span
Simply Supported Beam or Slab
According to Clause 22.2 of IS 456, the effective span of a simply supported beam or slab—one that is not integrated rigidly with its supports—can be determined in two ways:
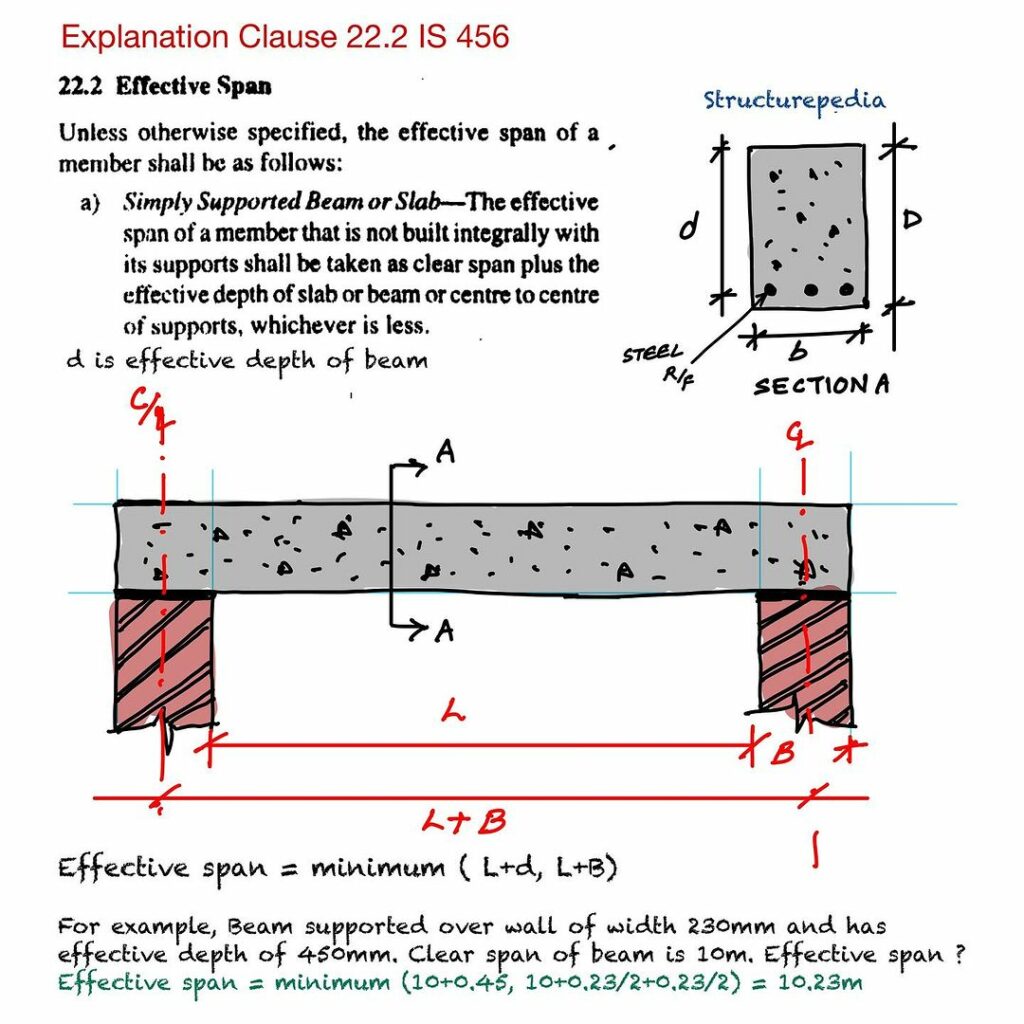
- Clear Span + Effective Depth: This method calculates the effective span as the sum of the clear span (distance between support faces) and the effective depth (d) of the beam or slab. The effective depth is the distance from the top of the beam to the center of the tension reinforcement.
- Centre-to-Centre of Supports: Alternatively, the effective span can be the distance measured from the center of one support to the center of the other. Effective Span Formula: Effective Span = min(Clear Span + d, Centre-to-Centre of Supports) The standard advises using the lesser value from these two methods as the effective span. This ensures a conservative approach, minimizing the risk of structural failure.
Example Calculation of Effective Span
Let’s consider an example to understand this concept better. Suppose a beam is supported on a wall with a width of 230 mm and has an effective depth (d) of 450 mm. The clear span (L) of the beam is 10 m (10,000 mm). Using the formula above:
- Clear Span + d: 10,000 mm + 450 mm = 10,450 mm
- Centre-to-Centre of Supports: 10,000 mm + 230/2 + 230/2 = 10,230 mm
Thus, the effective span will be: Effective Span = min(10,450 mm,10,230 mm) = 10,230 mm
This example illustrates how we choose the lesser value to determine the effective span.
Importance of the Effective Depth (d) in Calculations
In these calculations, the effective depth (d) of the beam or slab is critical. The effective depth is the distance from the top of the section to the centroid of the tension steel reinforcement. For most structural members, this depth impacts bending resistance and deflection characteristics. Selecting an accurate effective depth ensures the stability and strength of the beam under load, which is why it is a fundamental component in determining effective spans as outlined by IS 456.
Application in Structural Analysis
The effective span calculation influences various aspects of structural analysis:
- Bending Moment and Shear Force Calculation: The effective span defines the length over which these forces act. A longer effective span increases the bending moment and shear forces, necessitating additional reinforcement or stronger materials.
- Deflection Analysis: Deflection, or the vertical displacement under load, is directly influenced by the effective span. Shorter effective spans result in less deflection, contributing to a stiffer structure.
- Load Distribution and Material Economy: Properly calculated effective spans help in the optimal distribution of loads, which leads to material savings without compromising safety. Accurate span determination can reduce costs and make construction projects more efficient.