Understanding the centroid and moment of inertia of common shapes is essential in fields such as engineering, physics, and architecture. These properties are crucial in analyzing various structures and materials’ stability, balance, and resistance.
What is the Centroid?
The centroid of a shape is the geometric center or the “average” location of all the points in a shape. For regular, symmetrical shapes, the centroid is often located at the intersection of the axes of symmetry. However, for irregular shapes, calculating the centroid requires more complex methods. The centroid is a critical concept in engineering, as it affects how forces are distributed across a structure.
What is the Moment of Inertia?
The moment of inertia (I) measures an object’s resistance to rotational motion around an axis. It is determined by the distribution of mass within the object. The moment of inertia is crucial in understanding how an object will behave when subjected to rotational forces, such as in beams, rotating machinery, and vehicles.
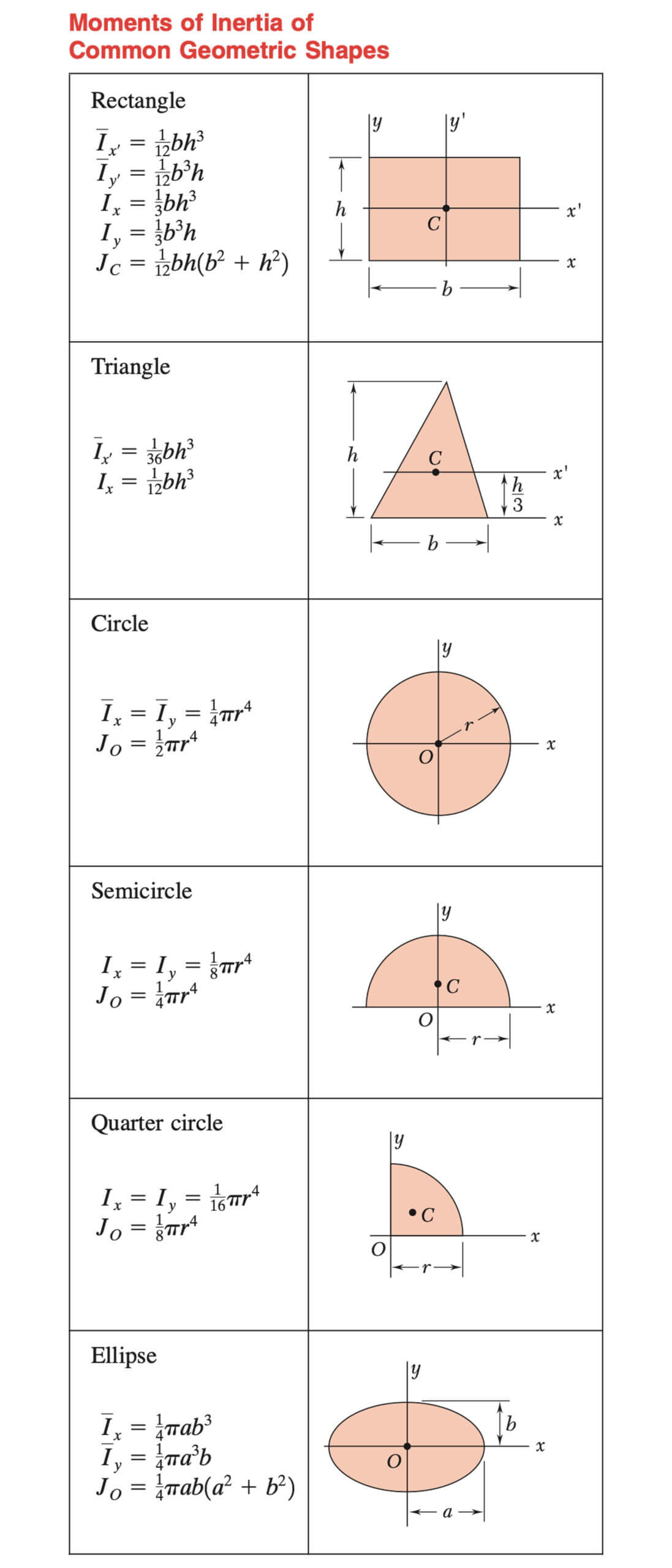
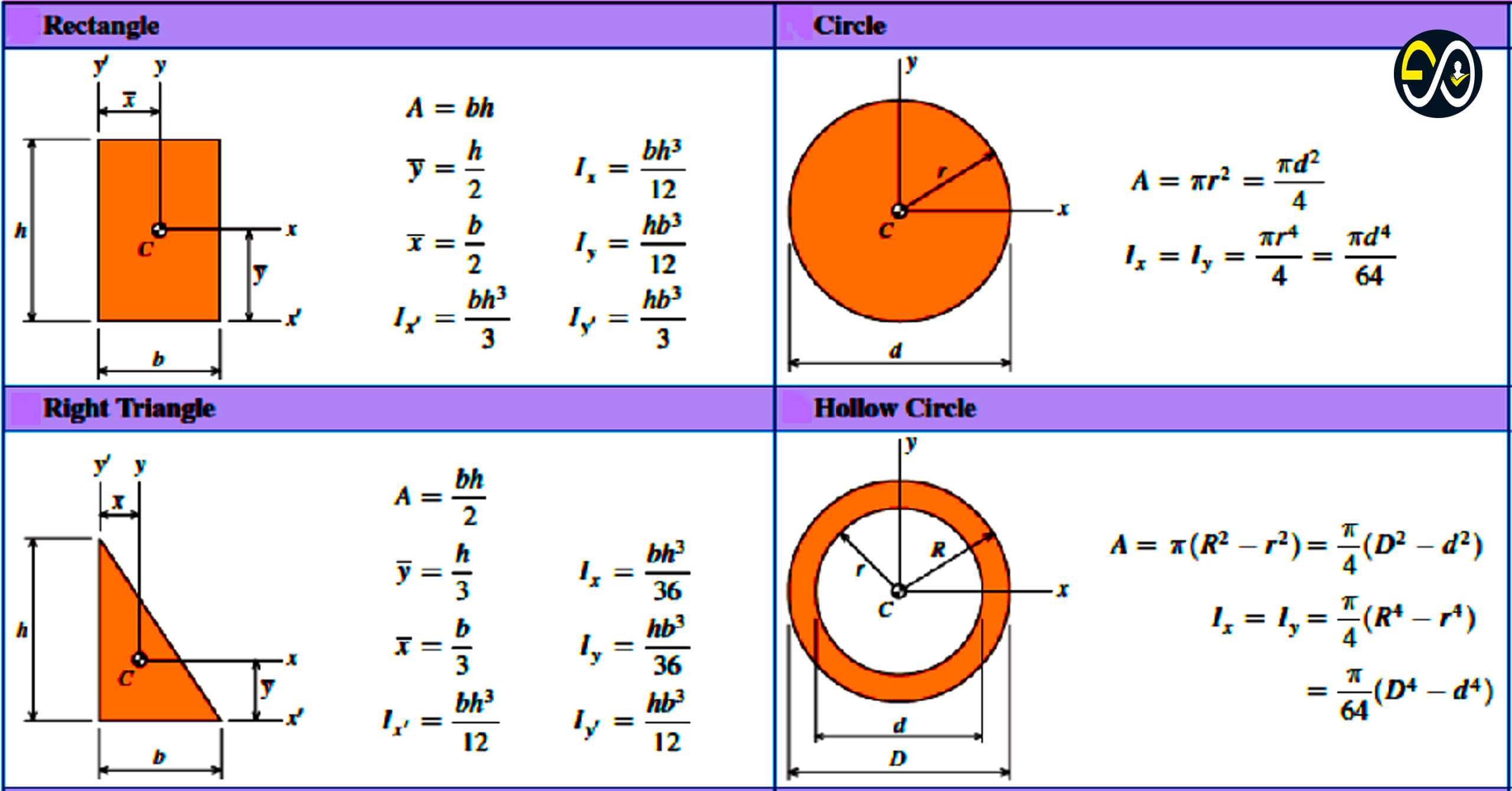
Rectangle
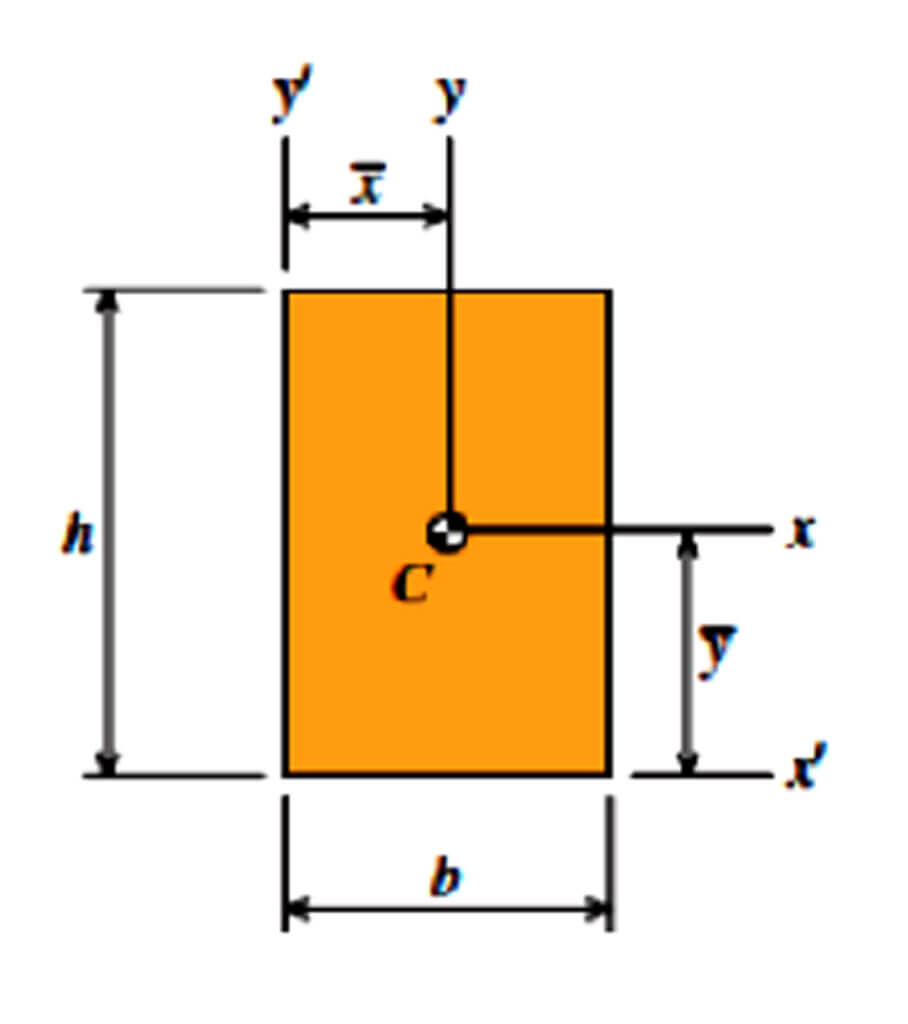
- A = bh
- ȳ = h/2
- x̄ = b/2
- Ix = bh3/12
- Iy = hb3/12
- Ix’ = bh3/3
- Iy’ = hb3/3
Right Triangle
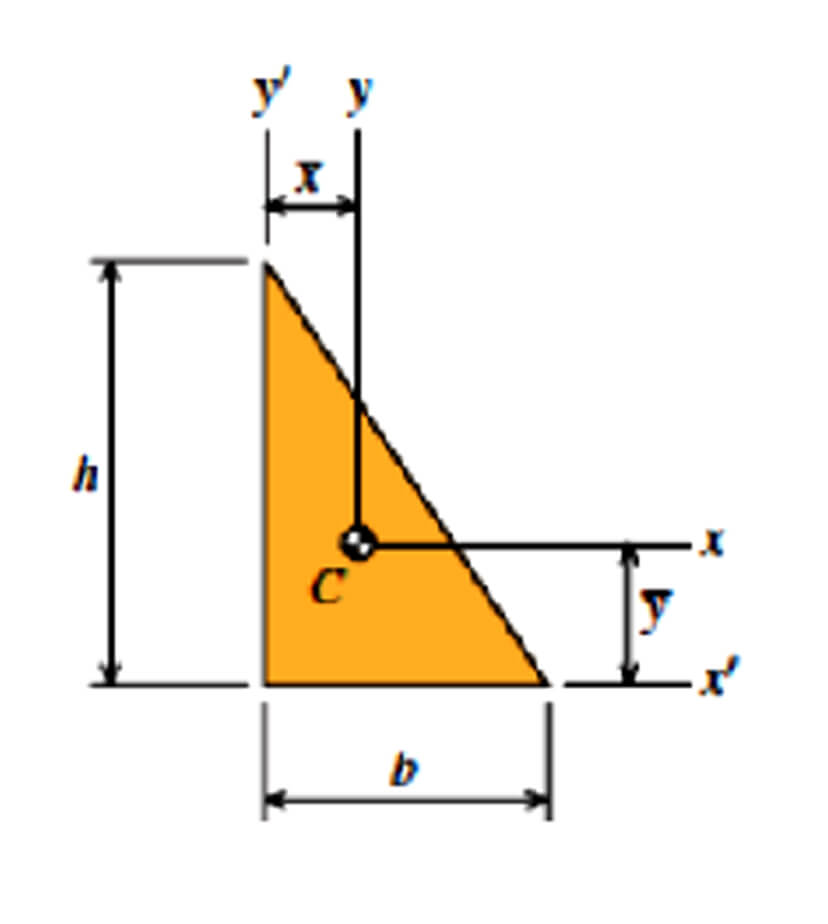
- A = bh/2
- ȳ = h/3
- x̄ = b/3
- Ix = bh3/36
- Iy = hb3/36
- Ix’ = bh3/12
- Iy’ = hb3/12
Triangle
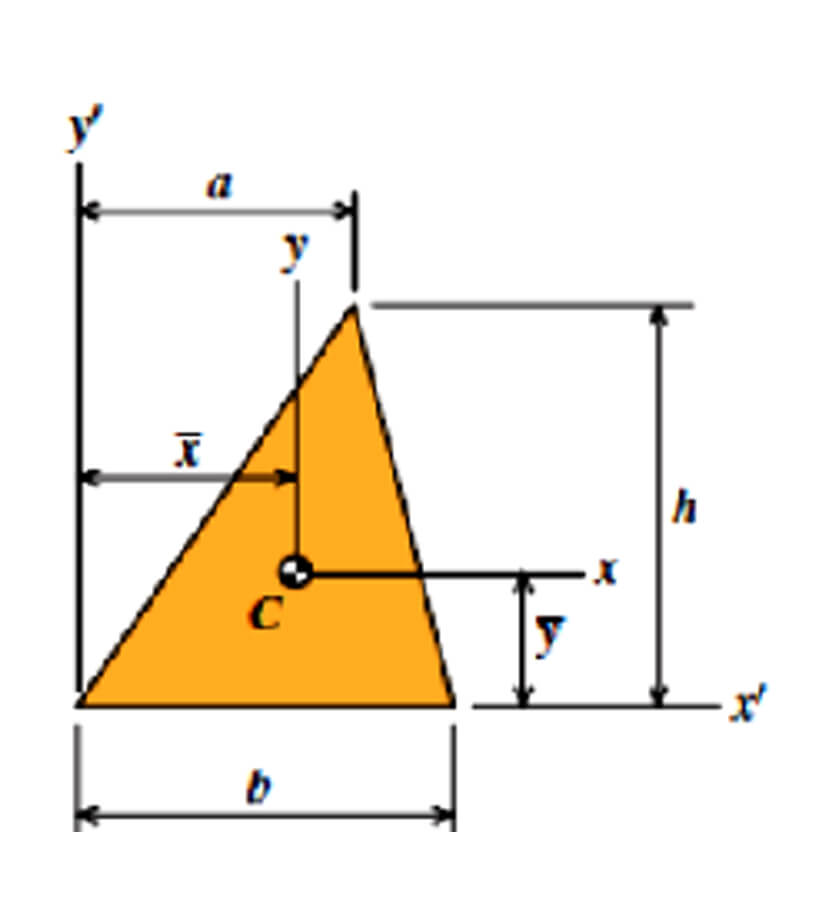
- A = bh/2
- ȳ = h/3
- x̄ = (a + b)/3
- Ix = bh3/36
- Iy = bh/36(a2 – ab + b2)
- Ix’ = bh3/12
Trapezoid
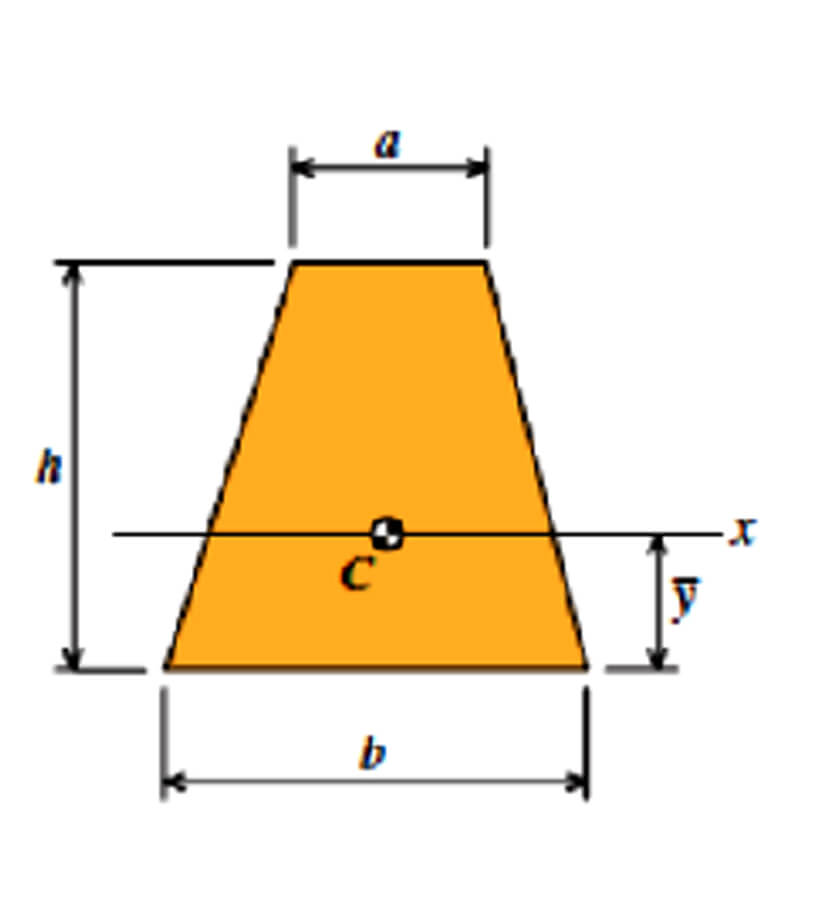
- A = ((a + b)h)/2
- ȳ = 1/3 * ((2a + b)/(a + b)) * h
- Ix = h3/(36(a + b)) * (a2 + 4ab + b2)
Semicircle
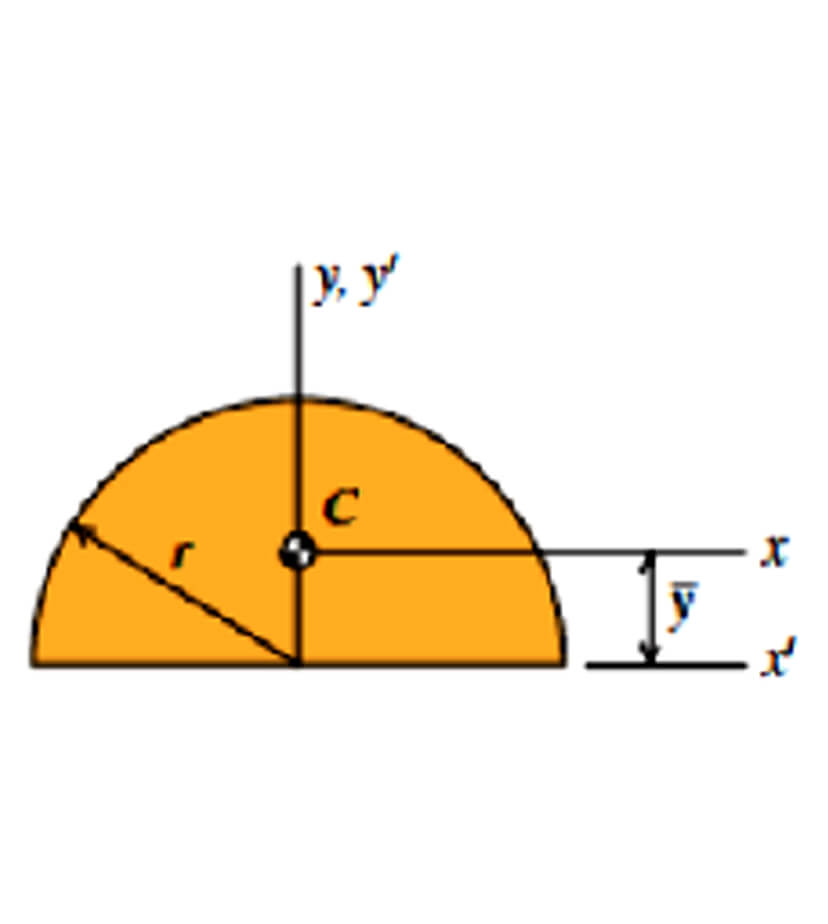
- A = 𝝅r2/2
- ȳ = 4r/3𝝅
- Ix = (𝝅/8 – 8/(9𝝅)) * r4
- Ix’ = Iy’ = 𝝅r4/8
Circle
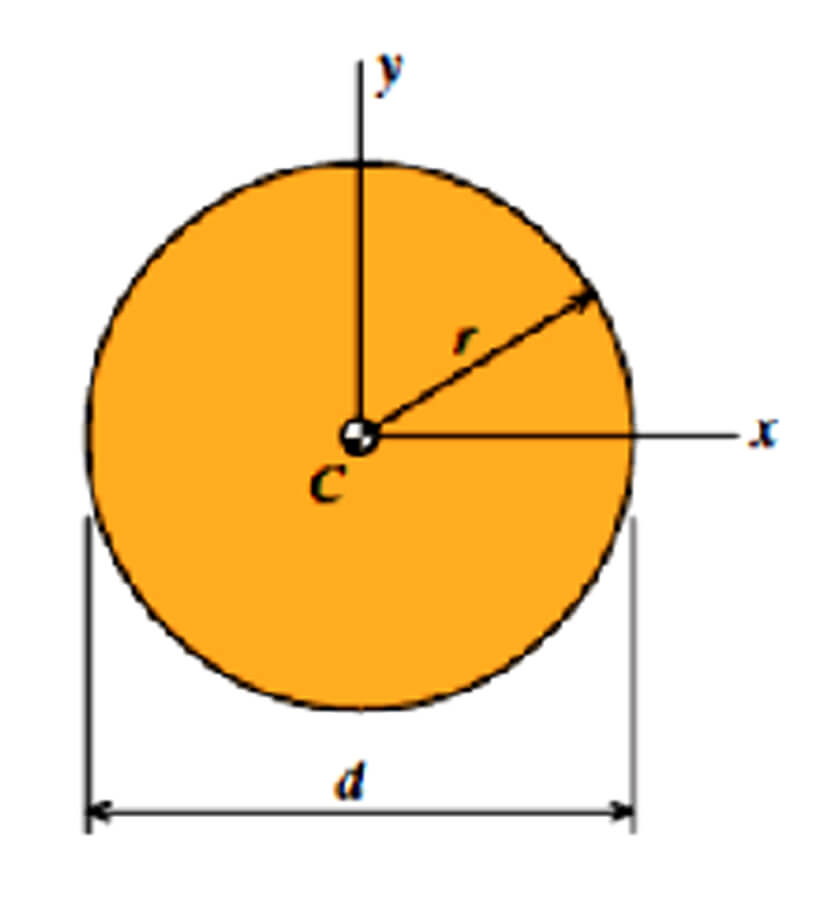
- A = 𝝅r2 = 𝝅d2/4
- Ix = Iy = 𝝅r4/4 = 𝝅d4/64
Hollow Circle
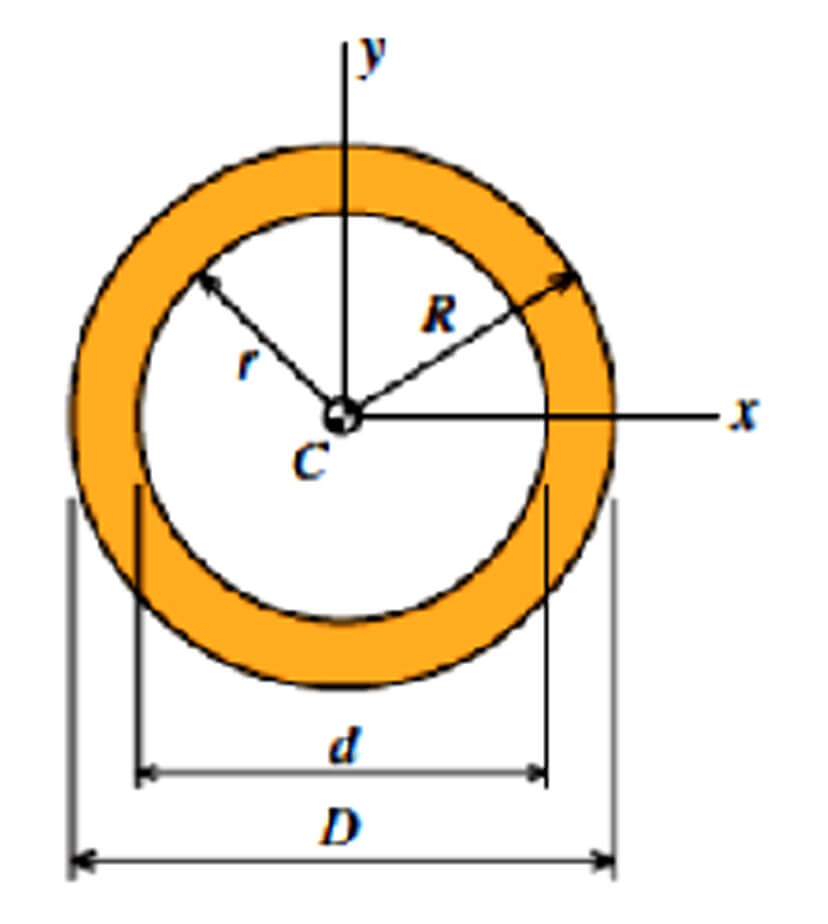
- A = 𝝅(R2 – r2) = 𝝅/4(D2 – d2)
- Ix = Iy = 𝝅/4 (R4 – r4) = 𝝅/64(D4 – d4)
Parabola
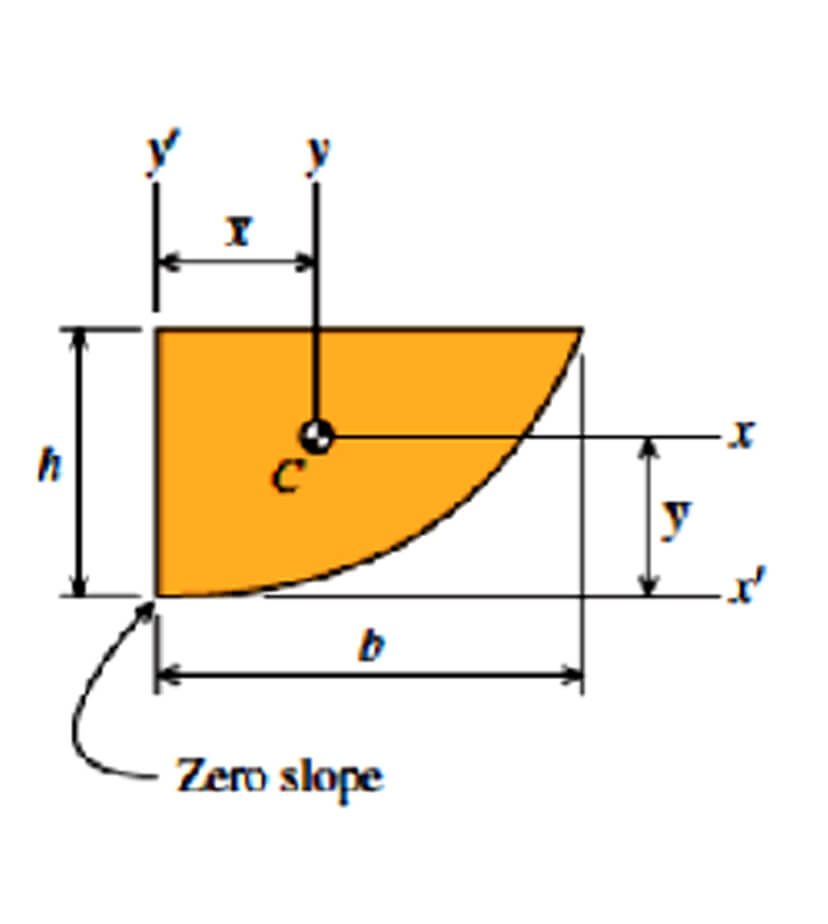
- A = 2bh/3
- y’ = h/b2 * x’2
- x̄ = 3b/8
- ȳ = 3h/5
Parabolic Spandrel
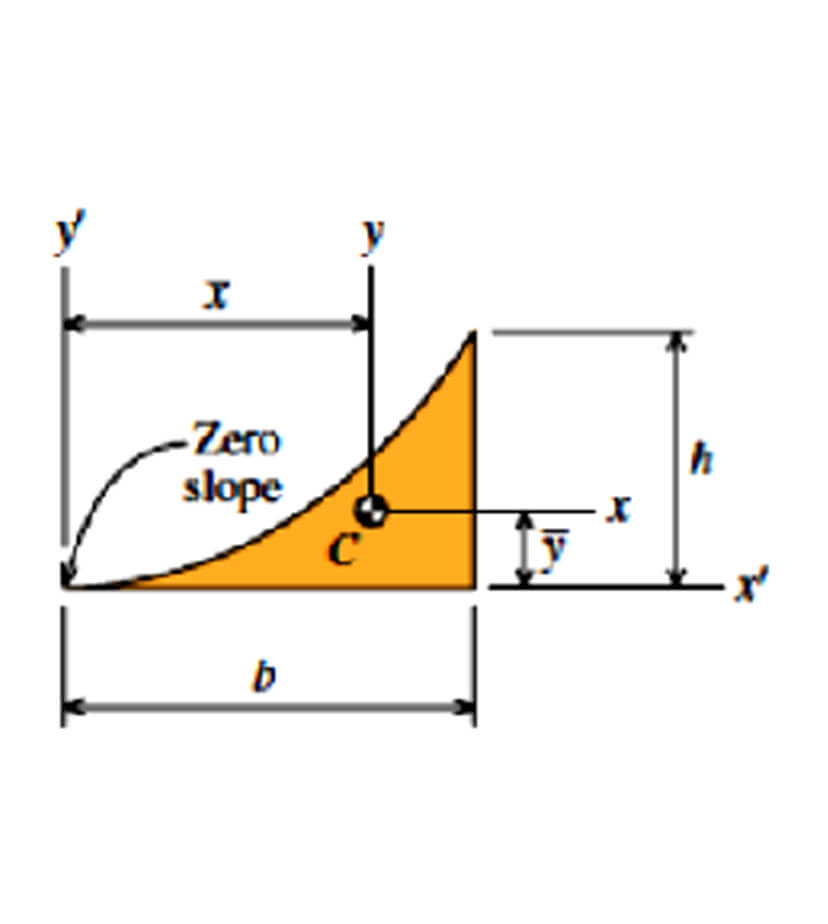
- A = bh/3
- y’ = h/b2 * x’2
- x̄ = 3b/4
- ȳ = 3h/10
General Spandrel
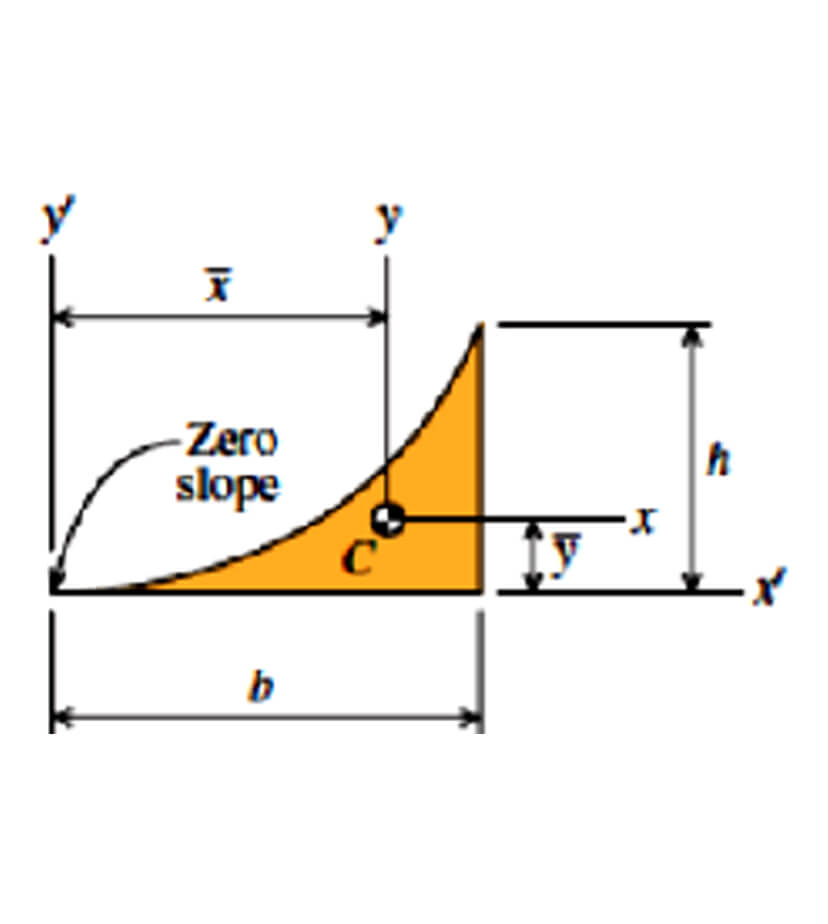
- A = bh/(n + 1)
- y’ = h/bn * x’n
- x̄ = (n + 1)/(n + 2) * b
- ȳ = (n + 1)/(4n + 2) * h