When it comes to structural engineering and concrete design, understanding load distribution in slabs is crucial for creating safe, functional, and efficient structures. In reinforced concrete construction, slabs are vital in transferring loads from the upper floors to the beams, columns, and foundations. Specifically, two-way slabs, which distribute loads in two directions, are commonly used in buildings with closely spaced supports. In this article, we delve into the concept of load distribution in two-way slabs, examining how forces are transferred to beams and supporting columns.
A two-way slab differs from a one-way slab in its load transfer mechanism, offering structural advantages for buildings with a square or nearly square floor plan. By the end of this article, you’ll gain a complete understanding of how load distribution works in two-way slabs, helping you achieve an optimal structural design.
What is a Two-Way Slab?
A two-way slab is a type of reinforced concrete slab that is supported on all four edges, allowing it to distribute loads in both the x (shorter) and y (longer) directions. When subjected to loads, these slabs transfer the load to the beams along both axes, which means the load is shared by beams on all four sides. This distribution mechanism reduces deflection and enhances structural efficiency, especially in buildings with square or nearly square bays.
Two-way slabs are typically used in areas with heavy loads or in structures requiring longer spans, such as shopping malls, residential apartments, and office buildings. The load distribution in these slabs depends on the slab’s aspect ratio (Ly/Lx) and the intensity of the load applied to it.
Key Parameters in Load Distribution for Two-Way Slabs
To analyze and design two-way slabs, several key parameters and concepts are used, including:
- Load Intensity (W): This refers to the intensity of uniformly distributed load (UDL) on the slab, measured in units like kN/m².
- Aspect Ratio (B = Ly/Lx): The aspect ratio (B) is the ratio of the longer span (Ly) to the shorter span (Lx). This parameter is crucial in determining the load distribution between the longer and shorter-span beams.
- Equivalent Uniform Distributed Load (UDL): The equivalent UDL represents how the load from the slab is divided for moments and shear forces on both long and short-span beams.
Load Distribution Mechanism in Two-Way Slabs

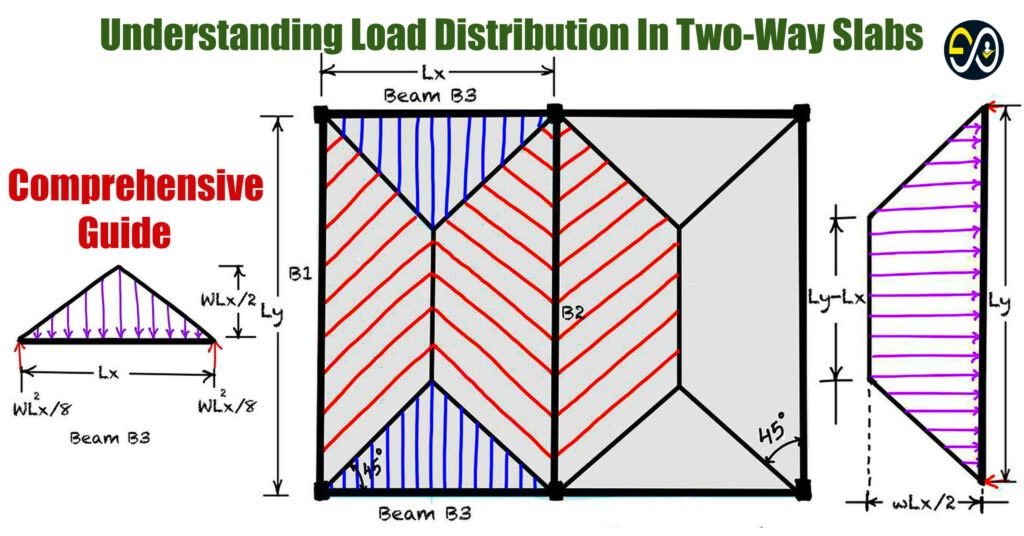
1. Load Transfer to Short Span Beams
In a two-way slab, a significant portion of the load is transferred to the short-span beams. The load distribution pattern is illustrated with shaded regions in the diagram above. Here’s a breakdown of the process:
- Bending Moment on Short Span Beam: For the short span, the equivalent UDL for bending moment is (2/3) x WLx/2, where:
- W is the intensity of UDL on the slab.
- Lx is the shorter span.
- Shear on Short Span Beam: The equivalent UDL for shear on the short span beam is (1/2) x WLx/2. This calculation helps engineers determine the required shear reinforcement on short-span beams to handle the load efficiently.
2. Load Transfer to Long Span Beams
While the short-span beams bear a significant portion of the load, the long-span beams also play a crucial role in supporting the slab. Here’s how the load is distributed along the longer-span beams:
- Bending Moment on Long Span Beam: For bending moment calculations on long span beams, the equivalent UDL is (1 – (1/3B)^2) x WLx/2.
- This equation considers the slab’s aspect ratio (B) to distribute the load accurately, ensuring that the beams can handle the induced bending moment.
- Shear on Long Span Beam: The equivalent UDL for shear on the long span beam is given by (1 – (1/2B)) x WLx/2. This value is essential for calculating shear reinforcements on the long-span beams.
By using these calculations, engineers can design beams with appropriate reinforcements to ensure the stability and durability of the slab system.
Significance of Load Distribution in Structural Design
Understanding load distribution in two-way slabs is essential in structural engineering for the following reasons:
- Efficient Load Transfer: Proper load distribution minimizes stress concentration on individual beams, reducing the risk of localized failures.
- Improved Structural Efficiency: Two-way slabs help optimize material usage, allowing for lighter slab designs without compromising on load-carrying capacity.
- Reduced Deflection: Two-way slabs experience lower deflection compared to one-way slabs, making them suitable for long-span applications.
- Enhanced Safety: Accurate load distribution calculations are critical in designing slabs that meet safety and building code requirements, ensuring the structure can withstand applied loads over its lifespan.
Practical Application of Load Distribution in Two-Way Slabs
In practice, two-way slabs are designed using analytical or numerical methods, such as finite element analysis (FEA), which accurately models load distribution across slabs. However, in conventional design scenarios, engineers often rely on approximate methods like the Direct Design Method or the Equivalent Frame Method to simplify calculations.
In the example shown in the diagram, the slab is divided into sections using 45° lines from the corners, indicating the portions of the load that each beam (both short and long spans) will carry. This approach is useful for quick calculations, especially in symmetrical structures with uniformly distributed loads.
Load Distribution Formulas Summary
To assist with quick reference, here’s a summary of the key formulas for load distribution in two-way slabs:
- Equivalent UDL for Bending Moment on Short Span Beam:
UDL= 2/3(WLx/2) - Equivalent UDL for Shear on Short Span Beam:
UDL=1/2(WLx/2) - Equivalent UDL for Bending Moment on Long Span Beam:
UDL=(1−13B2)(WLx/2) - Equivalent UDL for Shear on Long Span Beam:
UDL=(1−1/2B)(WLx/2)
These formulas provide a foundation for understanding and calculating load distribution, ensuring that the slab can handle applied loads safely and effectively.


Thanks for the information