
Steel bars are a fundamental component in construction, used to reinforce structures like buildings, bridges, and other large-scale projects. Whether you’re working on a home renovation or a massive skyscraper, knowing the weight of the steel bars you’re using is crucial. But why, you might ask? This information is essential for structural safety and cost estimation, as well as ensuring that materials are used efficiently and projects are completed within budget.
Steel is the most versatile commonly used structural material. The essential elements in steel are metallic iron and the element non-metallic carbon, with small quantities of other elements such as silicon, nickel, manganese, chromium, and copper. It is thus an alloy. Though steel is usually more than 90% iron, with other elements present in small quantities, these other elements have a pronounced effect on the properties of steel.
Unit weight of steel
It is the ratio of the weight of steel per unit volume. It is also called the specific weight of steel. Unit Weight of steel is 7850kg/m3 or 78.5kN/m3
The value of the unit weight of steel in different units.
Steel Unit Weight is measured in different units like 7850kg/m3, 78.50KN/m3, 7.850g/cm3, 290.74 lb/in3, and 490.059Ib/ft3.
The formulas provide the steel weight per unit length
1. The formula (D2/162) is utilized while the length is specified in meters.
2. The formula (D2/533) is utilized while the steel bar length is specified in feet.
1. D2/162 formula derivation for steel unit weight per meter
We have to calculate the unit weight of Steel rods in Kilogram per meter and we know that the unit weight of the steel bar is 7850kg/m3.
It means 7850kg is steel weight of 1 cubic meter.
Weight = Volume of steel x Density of steel bar
Weight = Cross-Sectional area x Length x Density of steel bar
W = π/4 x D2 x L x Density of steel bar
W = weight of steel (kg), π = 3.14, D = Diameter of Steel bar (mm), L = Length of steel bar (1m),
Density of bar = 7850kg/m3
Putting all the value we get
Weight = 3.14/4 x D2 x 1m x 7850kg/m3
Now we have to convert meters into millimeters
So weight = D2 x 3.14/4 x 1000 x 7850/1000 x 1000 x 1000
Weight = D2 x 0.00616225
It can be written as follows
Weight = D2/1 x 0.00616225/1 => D2/1/0.00616225 => D2/162.278 ≃ D2/162 kg/m
This formula applies only to the circular shape of the steel bars density is 7850kg/m³
(D2/162 x Length of steel bar (m)) This formula is used to find the weight of the steel bar in kg
Example:
If the diameter of the steel bar is equal to 16mm and the steel bar’s length of the steel bar is 12m then find the weight of the steel bar.
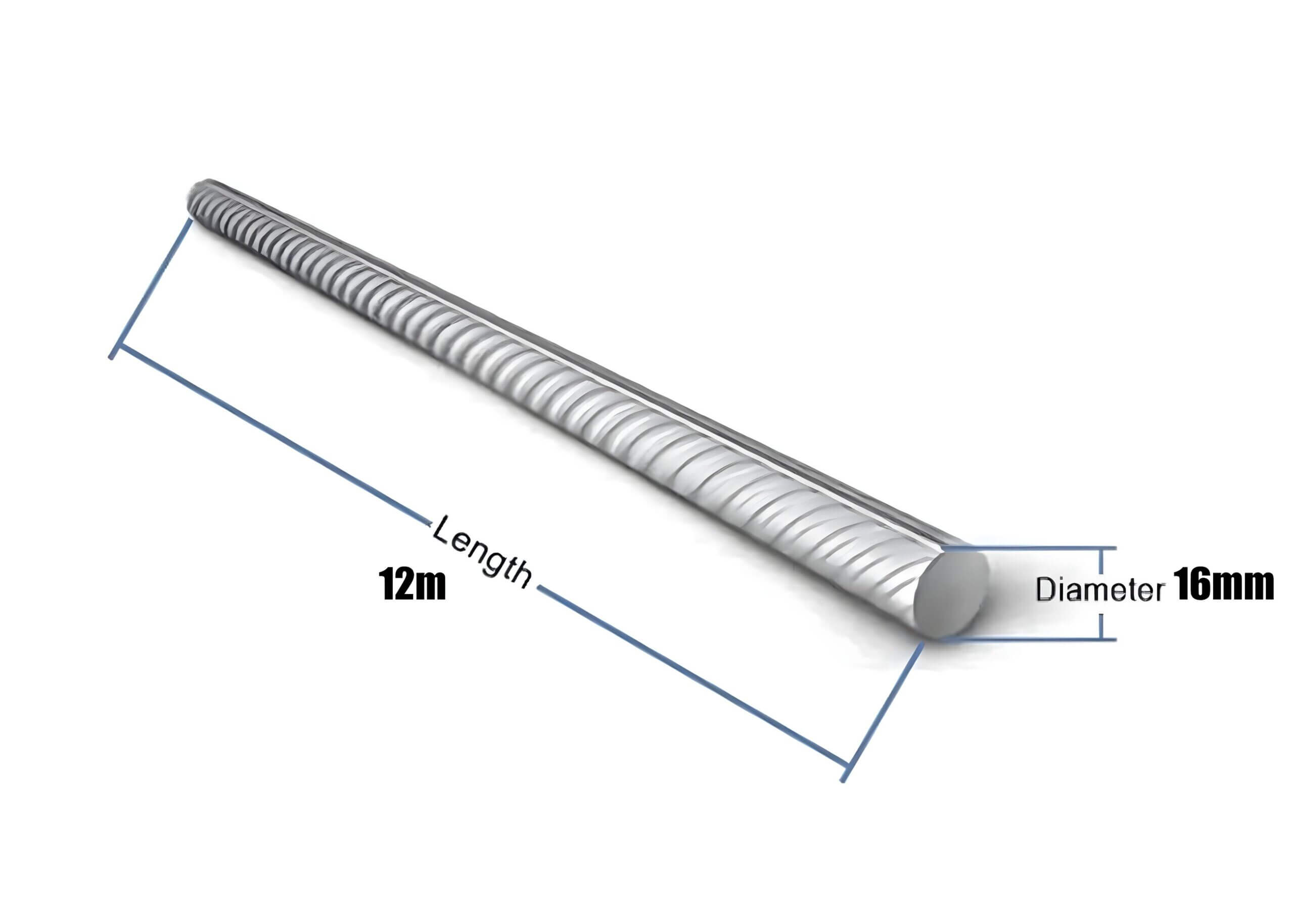
D2/162 x L => 16 x16/162 ×12 = 18.962kg
2. D2/533 formula derivation for steel unit weight per foot
Because of 1m =3.2804ft
Weight = D2/162 x 3.2804 ≃ D2/533 kg/ft
Weight =D2/533 x L (kg/ft)
This formula is used to calculate the steel weight per foot.
Example:
Calculate the weight of a steel bar having a diameter of 20mm and a length of 39.37ft.

Weight = D2/533 x L
Weight = 20 x 20/533 x 39.37 = 29.54kg
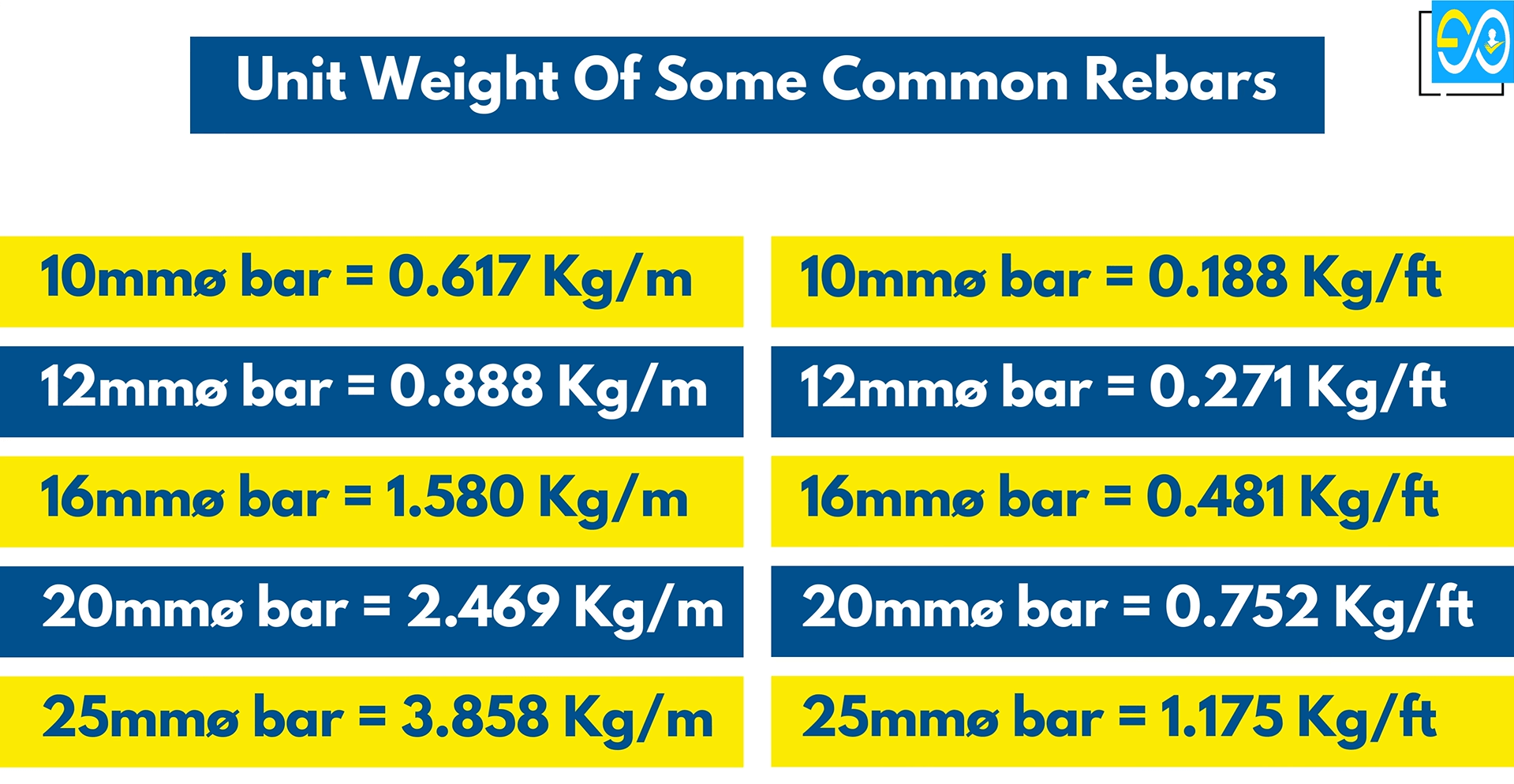
Unit Weight Of Some Common Rebars

Civil